|
|
|
|
Глубина
резко изображаемого пространства О глубине резко изображаемого пространства, безусловно, известно всем, кому приходилось держать в руках фото- или кинокамеру. Соответствующие формулы для расчетов можно легко отыскать в разных справочниках и статьях. Так зачем же мне понадобилось писать еще один текст на эту тему? Откровенно говоря, я преследовал две цели:
Конечно, многие люди, давно занимающиеся фотографией, могут легко оценить глубину резкости на основании своего практического опыта. Другие предпочитают ограничиваться просмотром снимаемого сюжета через объектив зеркальной камеры. Вряд ли эта статья поведает таким фотографам о чем-то новом. Действительно, интуиция и опыт порой оказываются при съемке гораздо важней. Тем же, у кого пока опыт не столь велик, а интуиция не столь развита, может быть полезно ознакомиться с нижеизложенным. Статья состоит из двух частей. В первой приведены формулы. Во второй - обсуждение этих формул. Если от одного вида математических выражений вам становится не по себе, переходите сразу к чтению второй части. Перед тем как перейти непосредственно к сути, замечу, что все приводимые ниже формулы приблизительны, то есть, основаны на ряде допущений. Например, они не учитывают различие в размерах входного и выходного зрачков объективов. Они также предполагают такую съемку, когда дистанция фокусировки существенно превосходит фокусное расстояние объектива. Но в подавляющем большинстве случаев все эти формулы можно использовать на практике. Рассмотрение более тонких деталей выходит за рамки данной статьи (макросъемка, применение специальной оптики и т.п.). В первой группе формул за точку отсчета принят снимаемый объект. Эти формулы позволяют ответить на вопрос: насколько далеко простирается область резкости перед объектом (Lперед) и за объектом (Lза):
Гиперфокальное расстояние можно рассчитать по следующей формуле:
Диаметр допустимого
круга нерезкости показывает, в пятно какого диаметра допустимо размыть
точку на негативе, чтобы для человеческого глаза она еще оставалась "точкой".
В обычной узкоформатной фотографии с кадром 24х36 мм часто полагают с=0,03
мм (это примерно 1/1500 от диагонали кадра). Такой диаметр круга нерезкости
позволяет просматривать снимок 13 х 18 см на расстоянии порядка Как видно, при d = h величина Lза становится равной бесконечности. Отрицательные значения Lза также следует рассматривать как бесконечную протяженность области резкости за объектом. Вторая группа формул позволяет вычислить величины d1 и d2, описывающие глубину резко изображаемого пространства в системе отсчета, где все расстояния измеряются от камеры:
Иными словами, все в пределах от d1 до d2 получится на снимке резким. После элементарных преобразований легко получить:
Опять-таки, если d больше или равно h, то d2 равно бесконечности. Третью группу формул удобно применять тогда, когда речь идет о съемках в одном масштабе. Например, фотограф решил снимать поясной портрет. Тем самым он уже определился относительно масштаба съемки. Как глубина резкости будет зависеть от фокусного расстояния объектива в этом случае? Вот для ответа на подобные вопросы и подходит третья группа формул. Строго говоря, под масштабом M понимают отношение линейного размера объекта на пленке к его реальному размеру. Если расстояние фокусировки существенно превышает фокусное расстояние объектива (что чаще всего справедливо), то масштаб M определяется следующей приближенной формулой:
Принимая во внимание это соотношение, а также формулу для гиперфокального расстояния, легко получить:
Или, что то же самое:
Наблюдательный читатель легко заметит, что эти формулы были получены из первой группы с помощью несложных преобразований. Применив аналогичные преобразования ко второй группе, можно было бы получить и четвертую группу формул. Но в любом деле главное - вовремя остановиться. Формулы третьей группы удобны для анализа, в то время как формулы первой и второй групп больше подходят для практических вычислений. Для целей данной статьи никакой нужды в других дополнительных формулах нет. Перейдем к обсуждению полезных выводов, которые следуют из приведенных выше формул. 1. Прежде всего, важно понимать, что нет никакой четкой границы между резким и нерезким в кадре. Все, что находится перед точкой фокусировки и за ней, в той или иной мере размыто. Когда говорят о глубине резко изображаемого пространства, то имеют в виду размер области, в которой размытость не превышает заданной величины. 2. Глубина резкости зависит, в общем случае, от масштаба съемки М, значения диафрагмы N и от соотношения d/h (то есть от отношения расстояния, на которое сфокусирован объектив, к гиперфокальному расстоянию). 3. Если гиперфокальное расстояние мало (то есть почти равно минимальному расстоянию фокусировки), то мы имеем дело с большой глубиной резкости. Строго говоря (по-научному), нельзя утверждать, что область от 1 м до бесконечности больше области от 2 м до бесконечности. Поэтому поясню, что я имею в виду. Пусть, например, h = 1 м и минимальная дистанция фокусировки объектива равна 1 м, тогда, очевидно, на чем бы мы ни сфокусировались, все получится резким. Дешевые камеры с фиксированной фокусировкой как раз снабжены объективами, сфокусированными на гиперфокальное расстояние. 4. Если объектив навести на бесконечность, то ближняя граница области резкости будет равна гиперфокальному расстоянию: d1 = h. 5. Если объект съемки находится на расстоянии, много меньшем, чем гиперфокальное (d << h или, что то же самое, c N << f M), то в этом случае (и только в этом случае) глубина резкости практически не зависит от фокусного расстояния объектива при неизменности M и N. Что значит много меньше? Ну, скажем, в 10 раз и более. Поясним сказанное на примерах. Пусть мы хотим снять предмет в масштабе М=0,1, то есть объект 24х36 см в полный кадр. Пусть мы выбрали диафрагму N=8. Тогда мы, может быть с удивлением, обнаружим, что глубина резкости для объектива f=200 мм будет почти точно такой же, как и для объектива f=50 мм, а именно где-то 2,5 см перед и 2,5 см за объектом. (Конечно же, мы приближались к объекту при переходе на короткофокусную оптику для сохранения масштаба). Другой пример: при N=8 снимаем портрет в масштабе M=0,05. В первом случае используем объектив с f=50 мм и получаем глубину резкости +11/-9 см. Во втором случае используем объектив 135 мм. В этом случае расчет дает глубину резкости +10/-9 см, то есть почти такую же, что и в первом случае. Эффект независимости глубины резкости от фокусного расстояния выражен тем сильней, чем больше масштаб М и меньше значение диафрагмы N. Так, если бы мы решили снимать в масштабе M=0,02 при N=16, то сразу бы заметили зависимость глубины резкости от фокусного расстояния. 6. При съемке на расстояниях фокусировки много меньших гиперфокального (d << h или, что то же самое, c N << f M) зона резкости расположена симметрично относительно объекта:
Отсюда видно, что при съемке на расстояниях много меньших гиперфокального, область резкости прямо пропорциональна диафрагменному числу N, то есть закручивание диафрагмы на одну ступень увеличивает область резкости в 1,4 раза. В других случаях эта зависимость носит более сложный характер. Полученные формулы можно переписать и в другом виде:
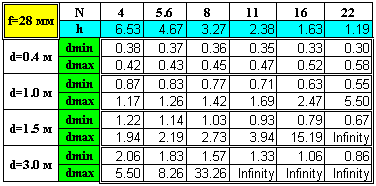
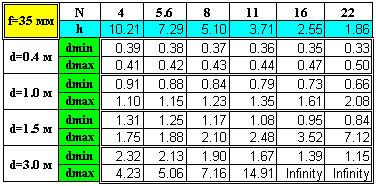
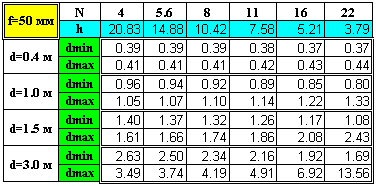
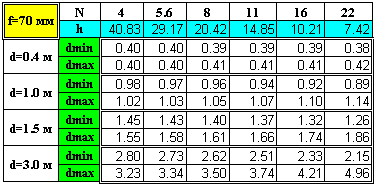
Еще раз подчеркну, что это приближенные формулы, точность которых тем выше, чем меньше d по сравнению с h. 7. По мере роста расстояния до объекта передняя зона резкости становится меньше задней. Когда d равно трети от гиперфокального расстояния, задняя глубина резкости в два раза превышает переднюю. 8. Как уже говорилось выше, при d=h задняя граница глубины резкости отодвигается в бесконечность. Полезно также знать, что в этом случае Lперед = d1 = h/2, то есть ближняя граница области резкости равна половине гиперфокального расстояния. 9. Если снимать объект двумя объективами в одном масштабе на расстояниях, сравнимых с гиперфокальным (то есть условие п. 5 не выполняется), то более короткофокусному объективу будет соответствовать большая задняя и меньшая передняя область резкости. *** Конечно, большое значение имеют не только резко изображаемые элементы фотоснимка, но и области с размытым изображением. При этом важна не только степень, но и характер размытия. Рисунок размытия зависит от многих конструктивных параметров объектива и не поддается простому математическому анализу. Степень же размытия фона при съемке заслуживает отдельной статьи и здесь не рассматривается. (См. мой текст под названием «Размываем фон по-научному».) Ясно, что ни начинающие, ни профессиональные фотографы не склонны постоянно заниматься вычислениями. Сам я последний раз вспомнил эти формулы, когда перешел на съемку так называемыми "зумами", на которых, конечно же, не было привычной для меня шкалы ГРИП. Тогда на каждый "зум" я заготовил соответствующие таблички, заламинировал их и стал носить в своем кофре. В качестве доступного справочного материала они показались мне довольно удобными. В качестве примера приведу такие таблички для объектива 28-70/4 (см. Приложение). При необходимости каждый может сам создать подобные таблички, ориентируясь на собственные потребности. Так, можно составить такие таблички для другого значения допустимого круга нерезкости, например, равного 0,02 мм. Это может иметь смысл, если предполагается печатать фотографии с большим увеличением. Замечу также, что, на мой взгляд, такие таблицы удобны не столь для получения конкретных цифр, сколь для быстрого получения общих оценок. Насколько увеличится глубина резкости при закручивании диафрагмы? Что произойдет при переходе на меньшие фокусные расстояния? Быстро получить ответы на подобные вопросы как раз и помогают описываемые мной таблички.
Что еще почитать
по данному вопросу? Остановлюсь, пожалуй, на двух текстах:
Вы также
можете воспользоваться для расчетов простым калькулятором на основе Рекомендую
также посетить
ПРИЛОЖЕНИЕ |
 |
 |
 |
 |
|
|
|
|
© Игорь Ефремов, 2002, все права сохранены
Для использования материалов этого сайта в коммерческих или некоммерческих
целях необходимо получить от меня письменное разрешение, если обратное
не оговорено в явной форме. |
|