|
|
|
|
Depth
of field Every person, who has ever dealt with a photo or movie camera, is familiar with the depth of field. This term describes the actual area, within which everything on a photograph will be acceptably sharp. The formulas to calculate this area can easily be found in various sources of information. Thus, you may ask: why did that guy decide to write another boring stuff? Frankly speaking, I was pursuing the following goals:
Of course, many photographers can determine the necessary depth of field from experience. There are also some people who prefer to use the DOF preview function of their SLR cameras. This text may not be very useful for them. Intuition and experience are truly very important factors. But I believe that those who have not had enough practice so far will find some useful data in this article. The text you are reading can be split into two parts. The first one gives the necessary formulas, while the second deals with the discussion of mathematical expressions. If math makes you feel sad, skip the formulas and read the conclusions. Before we get down to the subject matter, please note that all the formulas in this article are approximate, i.e. they are based on certain assumptions. For example, they do not take into account pupil magnification of lenses. They also assume that the distance between the object and the camera is significantly greater than the focal length. Nevertheless, the formulas you will find in this text hold true in many practical cases. Any subtle details are beyond the scope of this article. The formulas of the first group refer to the situation when all distances are measured from the object. They answer the question: how large are the areas of sharpness in front of and behind the object?
The hyperfocal distance can be calculated as:
The diameter
of the largest acceptable circle of confusion shows how large a point
can be on the image. In 35 mm photography, c is often assumed to be 0.03
mm (that is approximately 1/1500 of the image diagonal). If the confusion
circle is that small, one can comfortably look at a 5" x 7"
picture from the distance of one foot. Anyway, many depth of field scales
are based on this value. In digital photography, one has to decrease ±,
for example, to divide it by 10. Let us obtain a rough value for digital
photos. If we have a digital camera with a 1/2" imaging sensor that
consists of 2 ml. pixels, then at a rough estimate I'd say each pixel
is When d = h, the rear depth of field extends to infinity. This holds also for the cases when d is larger than h. The second group of formulas describes the depth of field in terms of distances calculated from the camera:
In other words, everything from d1 to d2 will be sharp on our photograph. Carrying out some algebraic manipulations yields:
Again, if d is greater or equal h, then d2 is infinity. When we are going to take pictures at constant object magnification, we may find it convenient to use the formulas of the third group. If we need a half-length portrait, for example, then magnification is given for us. How will depth of view depend on focal lengths of our lenses? The following formulas give the answer. Strictly speaking, magnification shows how small the image is if compared to the object. If the object distance is significantly longer than the focal distance of our lens (this holds true in most cases), then magnification M can be found from:
Taking this into account and recalling the formula for hyperfocal distance yields:
One can easily get a slightly different version after some transformations:
An observant reader can see that these formulas were obtained from the expressions of the first group. Similar transformations can also be applied to the second group. But I am not going to do so. It is very important to stop at the right moment. The formulas of the first and second groups are suitable for every day use, while the third group is convenient to analyze. We do not need any other formulas for the purposes of this article. Now let us draw some useful conclusions from all those formulas. 1. Generally speaking, depth of field is determined by the magnification M, f-number N, and the ratio of d to h. 2. If the hyperfocal length is small enough, i.e. almost equal to the minimum object distance, then we deal with a large area of sharpness. From the strict mathematical point of view, the area from 1 ft to infinity is not bigger than the area from 2 ft to infinity. So, I have to explain what I mean. Let us assume h = 3 ft and we have a lens with the minimum object distance of 3 ft. Then it is clear that irrespective of what we focus at everything will appear to be sharp on our picture. Cheap P&S cameras are usually equipped with lenses focused at the hyperfocal distance. 3. If the lens is focused at infinity, the distance to the closest sharp point equals the hyperfocal distance (i.e. d1 = h). 4. If object distances are short enough with respect to the hyperfocal distance (mathematically this fact is expressed as d << h or (c N) << (f M) ), then and only then depth of field does not depend on the focal length of our lenses. By saying "short enough" I mean at least 10 times smaller. Let us consider a couple of examples. If we want to make a picture of an object with dimensions of 9" x 14", then M=0.1. Let us set f-number to 8 (N=8). Under those conditions we may be astonished to see that depth of field is almost the same for a lens with f=200 mm and a lens with f=50 mm. It will be approximately an inch in front of the object and an inch behind it. (Of course, we had to move towards the object when shooting with a short focus lens to keep M constant.) Another example:
Suppose we want to make a portrait at N=8 (M=0.05). If we use a 50 mm
lens and a The focal length does not influence (to be more correct, insignificantly influences) depth of field as long as M is large enough and N is small enough. If we decide to shoot at M=0.02 and N=16, we will immediately notice that depth of field does depend on the focal distance. 5. Let us continue consideration of the case when d << h. Under such circumstances the area of sharpness is symmetrical.
Moreover, it is proportional to N. Thus, if we increase f-stop by one step, the depth of field will grow by 1.4 times. In other cases, the relation between depth of field and N is a little bit more complex. We can also rewrite the formula for the symmetrical depth of field in the following form:
Again, keep in mind that the formulas are approximations. The smaller the object distance in comparison to h, the more accurate they are. 6. As the object distance increases and becomes comparable to h, the rear depth of field gets larger than the front depth of field. When d = h/3, L behind = 2 L front. 7. It was mentioned above that when d = h, the rear depth of field extends to infinity. It is important to know that in this case L front = d1 = h/2, i.e. the front depth of field is half the hyperfocal distance. 8. If we shoot at a constant magnification (M=const) and d is comparable to h, then a lens with a shorter focal length will have a smaller front depth of field and larger rear depth of field at the same f-stop.
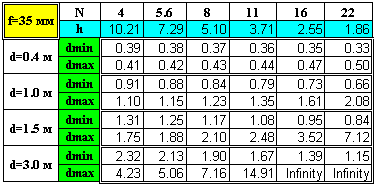
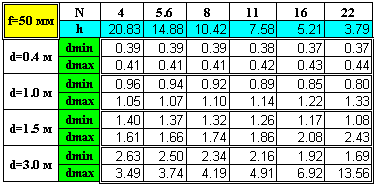
Of course, not only sharp objects matter. It is also interesting to analyze how blurred areas are represented on the picture. Both the degree and the quality of unsharpness are important. Subtle details, such as bokeh, are difficult to analyze. But the degree of fuzziness is quite easy to calculate. However, those issues will be discussed in a separate article ("Bluring the background. A scientific approach.") Of course, neither beginners nor pros tend to like making calculations constantly. As for me, I had to recall all those formulas a couple of years ago when I bought my first zoom lens. As a reasonable alternative to calculations you can also make up tables. They are easy to use and light to carry. I prepared an example of such tables for the 28-70 mm lens and placed it at the end of this article. Those tables can easily be customized to meet any specific needs. For example, you can compile your own tables based on smaller value of the circle of confusion. This makes sense if you are going to have large prints. I would say the tables are convenient not for exact calculations but for obtaining general estimates. How will changes in f-stop influence the depth of field? What will a smaller focal length result in? Such questions can easily be answered with the help of such tables.
Finally, I would like to mention a couple of other publications that deal with the lens theory:
You can also download a simple calculator in the form of an MS Excel file: Blur_02.xls. Also you
may use Don Fleming's DOF calculator:
APPENDIX |
 |
 |
 |
 |
|
|
|
|
® Igor Yefremov, 2002, all rights reserved You
must obtain a written permission from me to use any materials of this
site for any commercial or non-commercial purposes, unless there is an
explicit statement to the contrary. |
|